Puerto pesquero (6) — combustible

Entre las ideas planeadas a publicar cuando iniamos este sitio, una gasolinera era lo menos imaginable, pues coexisten en cualquier rincón que tenga carreteras — en algún momento de nuestras vidas, hemos vista una. ¿Para qué aludir lo conocido?

Lo anterior, además, tiene implícito la existencia de motores de combustión interna. Los propulsores de lanchas también usan energía para activar pistones.

Eso mismo nos motivó a incluir estas imágenes. Para continuar con el inventario de infraestructura y servicios necesarios en un puerto pesquero.

Puerto pesquero (5) — controles de caño

En “Hielo para pescadores” existen imágenes de la infraestructura necesaria para almacenar, levantar, triturar y dispensar hielo. Deseamos completar esa publicación, mostrando el control del caño de descarga.

Puerto pesquero (4) — atracaderos y bolardos

Los atracaderos transmiten firmeza, confianza, seguridad, permanencia y tranquilidad. Para ello, también el pescador debe fiar de sus ballestrinques.

ANOVA combinado (3) — diferentes épocas

La explicación de estos análisis se encuentra entre las paginas 177 – 180. Época de siembra dentro del año es incluida como variable de efectos fijos.

# Gráfico de barras  errores típicos
ggplot(MEDIAS,     aes(x  =  VARIEDAD, 
                       y  =  RENDIMIENTO, 
                    fill  =  EPOCA)) + 
       geom_bar(position  =  position_dodge(), stat = "identity") +   
  geom_errorbar(aes(ymin  =  RENDIMIENTO-se, 
                    ymax  =  RENDIMIENTO+se), 
                   width  =  .2, 
                position  =  position_dodge(.9))  +   
scale_fill_brewer(palette =  "Set1") + theme_minimal()

Nuestras preguntas en cada análisis ¿Qué más existirá disponible que aún nos falte emplear? ¿Habrán otros códigos simplificados y elegantes? Existen.

Códigos en R

#***********************************************************
# EXPERIMENTACIÓN EN AGRICULTURA                              
# Fernández Escobar, R.; Trapero, A.; Domínguez, J. 2010       
# CAPÍTULO 13: ANÁLISIS DE LA VARIANZA COMBINADO 
# Análisis de diferentes épocas (páginas 177 - 180) 
#************************************************************

#### Importar Tabla 13.3
InviernoPrimavera <- read.csv("C:/Users/Administrator/Desktop/tabla 13.3.csv", header=TRUE)
attach(InviernoPrimavera)
print(InviernoPrimavera)

##    VARIEDAD     EPOCA BLOQUE RENDIMIENTO
## 1        V1  Invierno      I           0
## 2        V1  Invierno     II         214
## 3        V1  Invierno    III         425
## 4        V1  Invierno     IV          40
## 5        V2  Invierno      I        1252
## 6        V2  Invierno     II         627
## 7        V2  Invierno    III         716
## 8        V2  Invierno     IV        1068
## 9        V3  Invierno      I        2163
## 10       V3  Invierno     II        2714
## 11       V3  Invierno    III        2521
## 12       V3  Invierno     IV        2240
## 13       V1 Primavera      I        1036
## 14       V1 Primavera     II         697
## 15       V1 Primavera    III         849
## 16       V1 Primavera     IV        1258
## 17       V2 Primavera      I        1524
## 18       V2 Primavera     II        1861
## 19       V2 Primavera    III        2220
## 20       V2 Primavera     IV        1744
## 21       V3 Primavera      I        1312
## 22       V3 Primavera     II         874
## 23       V3 Primavera    III         695
## 24       V3 Primavera     IV        1133

#### Agregando función para calcular estadísticas descriptivas de interacciones
library(plyr)

source("C:/Users/Administrator/Desktop/summarySE.r") 
MEDIAS <- summarySE(InviernoPrimavera, measurevar="RENDIMIENTO", groupvars=c("VARIEDAD", "EPOCA"))
MEDIAS

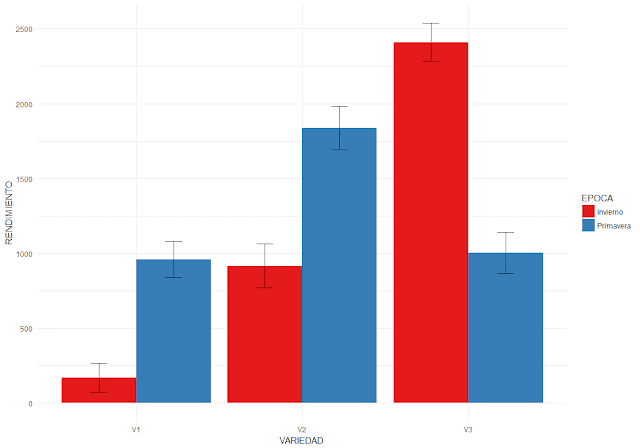
##   VARIEDAD     EPOCA N RENDIMIENTO       sd        se       ci
## 1       V1  Invierno 4      169.75 193.8735  96.93673 308.4959
## 2       V1 Primavera 4      960.00 242.2602 121.13010 385.4900
## 3       V2  Invierno 4      915.75 294.1206 147.06029 468.0115
## 4       V2 Primavera 4     1837.25 290.9082 145.45410 462.8999
## 5       V3  Invierno 4     2409.50 254.7188 127.35940 405.3145
## 6       V3 Primavera 4     1003.50 273.1819 136.59093 434.6933

#### Gráficos 
library(ggplot2)

# Gráfico de barras  errores típicos
ggplot(MEDIAS,     aes(x  =  VARIEDAD, 
                       y  =  RENDIMIENTO, 
                    fill  =  EPOCA)) + 
       geom_bar(position  =  position_dodge(), stat = "identity") +   
  geom_errorbar(aes(ymin  =  RENDIMIENTO-se, 
                    ymax  =  RENDIMIENTO+se), 
                   width  =  .2, 
                position  =  position_dodge(.9))  +   
scale_fill_brewer(palette =  "Greens") + theme_minimal()

#### Diagrama de dispersión
ggplot(InviernoPrimavera, aes(x=EPOCA, y=RENDIMIENTO, color=VARIEDAD)) + 
  geom_point(shape=1) + scale_color_brewer(palette = "Set1") +
  geom_point(size = 3.0)

#### Gráfico de lineas
ggplot(MEDIAS, aes(x = factor(EPOCA), y = RENDIMIENTO, colour = VARIEDAD, group = VARIEDAD)) +
  scale_color_brewer(palette = "Set1") + geom_line(size = 1.0, linetype = 'solid')

#### Gráfico de lineas + errores típicos
pd <- position_dodge(0.1) # mover barras de errores .05 hacia la izquierda y la derecha
SEgraph <- ggplot(data = MEDIAS, aes(x = EPOCA, y = RENDIMIENTO,
                                     group    = VARIEDAD, 
                                     color    = VARIEDAD, 
                                     linetype = VARIEDAD, 
                                     shape    = VARIEDAD))                          + 
  geom_errorbar(aes(ymin =  RENDIMIENTO-se,     ymax     = RENDIMIENTO+se), 
                width    =  .2, position = pd,  size     = 0.4, linetype = 'solid') +
  geom_line(position     =  pd, size     = 1.0, linetype = 'solid')                 + 
  geom_point(position    =  pd, size     = 3.0)                                     +     
  scale_color_brewer(palette = "Set1") + theme_minimal()                            + 
  ggtitle("Gráfico con errores típicos")                                            +
  xlab("EPOCA") + ylab("RENDIMIENTO(kg/ha)"); SEgraph

#### Boxplot y líneas de interacción
library("plyr")
ipMEDIAS <- ddply(InviernoPrimavera,.(EPOCA,VARIEDAD), summarise, val = mean(RENDIMIENTO)) # precalculando medias
ggplot(InviernoPrimavera, aes(x = factor(EPOCA), y = RENDIMIENTO, colour = VARIEDAD))               + 
  geom_boxplot() + geom_point(data = ipMEDIAS, aes(y = val), position = position_dodge(width=0.75)) +
  geom_line(data = ipMEDIAS, aes(y = val, group = VARIEDAD), position = position_dodge(width=0.75)) + 
  scale_x_discrete("Época") + scale_y_continuous("Rendimiento (kg/ha)") + theme_bw() + theme_bw()   +
  theme(axis.title.x = element_text(size = 12, hjust = 0.54, vjust = 0),
        axis.title.y = element_text(size = 12, angle = 90,  vjust = 0.25))

#### Boxplot para interacciones
library(plotly)

# EPOCA:VARIEDAD
gInvPrim <- plot_ly(InviernoPrimavera, y = ~RENDIMIENTO, color = ~EPOCA:VARIEDAD,  type = "box", 
             boxpoints = "all", jitter = 0.3, pointpos = -1.8); gInvPrim

# VARIEDAD:EPOCA
gInvPrim <- plot_ly(InviernoPrimavera, y = ~RENDIMIENTO, color = ~VARIEDAD:EPOCA,  type = "box", 
             boxpoints = "all", jitter = 0.3, pointpos = -1.8); gInvPrim

#### ANOVA para el rendimiento en Invierno
# Separando datos de Invierno
invierno <- InviernoPrimavera[1:12, ]; invierno

##    VARIEDAD    EPOCA BLOQUE RENDIMIENTO
## 1        V1 Invierno      I           0
## 2        V1 Invierno     II         214
## 3        V1 Invierno    III         425
## 4        V1 Invierno     IV          40
## 5        V2 Invierno      I        1252
## 6        V2 Invierno     II         627
## 7        V2 Invierno    III         716
## 8        V2 Invierno     IV        1068
## 9        V3 Invierno      I        2163
## 10       V3 Invierno     II        2714
## 11       V3 Invierno    III        2521
## 12       V3 Invierno     IV        2240

# Estadísticas descriptivas para VARIEDAD
library(doBy) 

## Warning: package 'doBy' was built under R version 3.3.2

library(pastecs)

summaryBy(RENDIMIENTO ~ VARIEDAD, data = invierno, FUN = stat.desc)

# Boxplot para rendimiento de variedades en invierno
gInvierno <- plot_ly(invierno, y = ~RENDIMIENTO, color = ~VARIEDAD,  type = "box", 
             boxpoints = "all", jitter = 0.3, pointpos = -1.8); gInvierno

# ANOVA Diseño en Bloques al Azar
ANOVAinvierno <- aov(RENDIMIENTO ~ BLOQUE + VARIEDAD, data = invierno) 
summary(ANOVAinvierno)

##             Df   Sum Sq Mean Sq F value   Pr(>F)    
## BLOQUE       3    19833    6611   0.073 0.972561    
## VARIEDAD     2 10405714 5202857  57.060 0.000125 ***
## Residuals    6   547094   91182                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

#### ANOVA para el rendimiento en Primavera
# Separando datos de Primavera
primavera <- InviernoPrimavera[13:24, ]; primavera

##    VARIEDAD     EPOCA BLOQUE RENDIMIENTO
## 13       V1 Primavera      I        1036
## 14       V1 Primavera     II         697
## 15       V1 Primavera    III         849
## 16       V1 Primavera     IV        1258
## 17       V2 Primavera      I        1524
## 18       V2 Primavera     II        1861
## 19       V2 Primavera    III        2220
## 20       V2 Primavera     IV        1744
## 21       V3 Primavera      I        1312
## 22       V3 Primavera     II         874
## 23       V3 Primavera    III         695
## 24       V3 Primavera     IV        1133

# Estadísticas descriptivas para PRIMAVERA
summaryBy(RENDIMIENTO ~ VARIEDAD, data = primavera, FUN = stat.desc)

# Boxplot para rendimiento de variedades en primavera
gPrimavera <- plot_ly(primavera, y = ~RENDIMIENTO, color = ~VARIEDAD,  type = "box", 
             boxpoints = "all", jitter = 0.3, pointpos  = -1.8); gPrimavera

# ANOVA Diseño en Bloques al Azar
ANOVAinvierno <- aov(RENDIMIENTO ~ BLOQUE + VARIEDAD, data = primavera) 
summary(ANOVAinvierno)

##             Df  Sum Sq Mean Sq F value Pr(>F)  
## BLOQUE       3   84709   28236   0.298 0.8262  
## VARIEDAD     2 1955465  977733  10.308 0.0115 *
## Residuals    6  569129   94855                 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

#### Modelo EPOCA EPOCA*REP(E) VARIEDAD VARIEDAD*EPOCA
# Opción 1
MODELO <- aov(RENDIMIENTO ~ EPOCA + Error(EPOCA/BLOQUE) + EPOCA*VARIEDAD, InviernoPrimavera)
summary(MODELO)

# Opción 2
MODELO <- aov(RENDIMIENTO ~ EPOCA + EPOCA/BLOQUE + EPOCA*VARIEDAD, InviernoPrimavera)
summary(MODELO)

##                Df  Sum Sq Mean Sq F value   Pr(>F)    
## EPOCA           1   62322   62322   0.670    0.429    
## VARIEDAD        2 5522514 2761257  29.685 2.26e-05 ***
## EPOCA:BLOQUE    6  104542   17424   0.187    0.975    
## EPOCA:VARIEDAD  2 6838665 3419332  36.760 7.63e-06 ***
## Residuals      12 1116223   93019                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

#### Descomposición de las sumas de cuadrados
#### de ambos factores en CONTRASTES ORTOGONALES,
#### con un grado de libertad

# Verificar niveles y orden de tratamientos
str(InviernoPrimavera)

# Coeficientes de contraste
# Contraste                  V1   V2   V3;
# V3 vs. V1 + V2  VARIEDAD   -1   -1    2;
# V1 + V2         VARIEDAD    1   -1    0;

# Crear matrix temporal
contrastmatrix <- cbind(c(-1, -1,  2), 
                        c( 1, -1,  0)); contrastmatrix

# Asignar matrix temporal a VARIEDAD
contrasts(InviernoPrimavera$VARIEDAD)<-contrastmatrix
InviernoPrimavera$VARIEDAD

# Correr nuevamente el ANOVA con interacciones
CONTRASTAR <- aov(RENDIMIENTO ~ EPOCA + EPOCA/BLOQUE + EPOCA*VARIEDAD, InviernoPrimavera)

# Separar suma de cuadrados para VARIEDAD
summary(CONTRASTAR, split = list(VARIEDAD = list("V3 vs. V1 + V2" = 1,"V1 + V2" = 2)))

##                                  Df  Sum Sq Mean Sq F value   Pr(>F)    
## EPOCA                             1   62322   62322   0.670 0.429009    
## VARIEDAD                          2 5522514 2761257  29.685 2.26e-05 ***
##   VARIEDAD: V3 vs. V1 + V2        1 2887574 2887574  31.043 0.000122 ***
##   VARIEDAD: V1 + V2               1 2634941 2634941  28.327 0.000182 ***
## EPOCA:BLOQUE                      6  104542   17424   0.187 0.974684    
## EPOCA:VARIEDAD                    2 6838665 3419332  36.760 7.63e-06 ***
##   EPOCA:VARIEDAD: V3 vs. V1 + V2  1 6821438 6821438  73.334 1.86e-06 ***
##   EPOCA:VARIEDAD: V1 + V2         1   17227   17227   0.185 0.674574    
## Residuals                        12 1116223   93019                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Códigos en SAS

/***********************************************************

 EXPERIMENTACIÓN EN AGRICULTURA                             

 Fernández Escobar, R.; Trapero, A.; Domínguez, J. 2010      

 CAPÍTULO 13: ANÁLISIS DE LA VARIANZA COMBINADO

 Análisis de diferentes épocas (páginas 177 - 180) 

************************************************************/

DATA InviernoPrimavera;

INPUT VARIEDAD $ EPOCA $ BLOQUE $ RENDIMIENTO;

CARDS;

V1     Invierno     I      0

V1     Invierno     II     214

V1     Invierno     III    425

V1     Invierno     IV     40

V2     Invierno     I      1252

V2     Invierno     II     627

V2     Invierno     III    716

V2     Invierno     IV     1068

V3     Invierno     I      2163

V3     Invierno     II     2714

V3     Invierno     III    2521

V3     Invierno     IV     2240

V1     Primavera    I      1036

V1     Primavera    II     697

V1     Primavera    III    849

V1     Primavera    IV     1258

V2     Primavera    I      1524

V2     Primavera    II     1861

V2     Primavera    III    2220

V2     Primavera    IV     1744

V3     Primavera    I      1312

V3     Primavera    II     874

V3     Primavera    III    695

V3     Primavera    IV     1133

;

ODS HTML;

* Imprimiento datos completos: Invierno y Primavera;

PROC PRINT;

PROC MEANS MEAN STD STDERR MAXDEC=2;

       VAR RENDIMIENTO;

       CLASS VARIEDAD EPOCA;

RUN;

*Ordenando y clasificando datos por VARIEDAD;

PROC SORT DATA = InviernoPrimavera; BY VARIEDAD; RUN;

PROC UNIVARIATE DATA = InviernoPrimavera; VAR RENDIMIENTO; BY VARIEDAD EPOCA;

RUN;

* Separando datos de Invierno;

DATA Invierno;

       SET InviernoPrimavera(obs = 12); RUN; *Incluye las primeras 12 líneas;

PROC PRINT DATA=Invierno;

RUN;

* ANOVA Diseño Bloques al Azar: Datos de Invierno;

PROC GLM DATA = Invierno;

       CLASS VARIEDAD BLOQUE;

       MODEL RENDIMIENTO = BLOQUE VARIEDAD;

RUN;

* Separando datos de Primavera;

DATA Primavera;

       SET InviernoPrimavera(firstobs = 13); RUN; *Datos inician en línea 13;

PROC PRINT DATA=Primavera;

RUN;

* ANOVA Diseño Bloques al Azar: Datos de Primavera;

PROC GLM DATA = Primavera;

       CLASS VARIEDAD BLOQUE;

       MODEL RENDIMIENTO = BLOQUE VARIEDAD;

RUN;

* Modelo EPOCA EPOCA*REP(E) VARIEDAD VARIEDAD*EPOCA

* Opción 1: ANOVA Combinado RENDIMIENTO (página 179);

PROC GLM DATA = InviernoPrimavera;

       CLASS VARIEDAD BLOQUE EPOCA;

       MODEL RENDIMIENTO = EPOCA BLOQUE EPOCA*BLOQUE VARIEDAD EPOCA*VARIEDAD;

RUN;

* Opción 2: ANOVA Combinado RENDIMIENTO (página 179) Mejor!;

PROC MIXED DATA = InviernoPrimavera METHOD = TYPE1;

       CLASS VARIEDAD BLOQUE EPOCA;

       MODEL RENDIMIENTO = EPOCA VARIEDAD EPOCA*VARIEDAD / DDFM=SATTERTH;

       RANDOM EPOCA*BLOQUE;

RUN;

* Modelo EPOCA EPOCA*REP(E) VARIEDAD VARIEDAD*EPOCA

* Opción 1: ANOVA Combinado RENDIMIENTO (página 180);

PROC GLM DATA = InviernoPrimavera;

       CLASS VARIEDAD BLOQUE EPOCA;

       MODEL RENDIMIENTO = EPOCA BLOQUE EPOCA*BLOQUE VARIEDAD EPOCA*VARIEDAD / SOLUTION;

       RANDOM EPOCA*BLOQUE / TEST;

       *Contrastes ortogonales: Variedades   V1  V2   V3;

       CONTRAST 'V3 vs. V1 + V2'  VARIEDAD  -1   -1   2;

       CONTRAST 'V1 vs. V2'       VARIEDAD   1   -1   0;

       *Época * Variedad                                   V1I V1P V2I V2P V3I V3P;      

       CONTRAST 'Época  : (V3 vs. V1 + V2)' VARIEDAD*EPOCA  -1   1  -1   1   2  -2 ;

       CONTRAST 'Época : (V1 vs. V2)'       VARIEDAD*EPOCA   1  -1  -1   1   0   0 ;

RUN;

* Opción 2: ANOVA Combinado RENDIMIENTO (página 180) Mejor!;

PROC MIXED DATA = InviernoPrimavera METHOD = TYPE1;

       CLASS VARIEDAD BLOQUE EPOCA;

       MODEL RENDIMIENTO = EPOCA VARIEDAD EPOCA*VARIEDAD / DDFM=SATTERTH;

       RANDOM EPOCA*BLOQUE;

       *Contrastes ortogonales: Variedades   V1  V2   V3;

       CONTRAST 'V3 vs. V1 + V2'  VARIEDAD  -1   -1   2;

       CONTRAST 'V1 + V2'         VARIEDAD   1   -1   0;

       *Época * Variedad                                   V1I V1P V2I V2P V3I V3P;      

       CONTRAST 'Época : (V3 vs. V1 + V2)' VARIEDAD*EPOCA  -1   1  -1   1   2  -2 ;

       CONTRAST 'Época : (V1 vs. V2)'      VARIEDAD*EPOCA   1  -1  -1   1   0   0 ;

RUN;

QUIT;

ODS HTML CLOSE;

--------------------------------------------

Archivos adjuntos:
Datos :  tabla 13.3.csv
R       :  capítulo 13c.R, summarySE.R
SAS    :  capítulo 13c.sas