La explicación de estos análisis se encuentra entre las paginas 177 – 180. Época de siembra dentro del año es incluida como variable de efectos fijos.
Nuestras
preguntas en cada análisis ¿Qué más existirá disponible que aún nos falte
emplear? ¿Habrán otros códigos simplificados y elegantes?
Códigos en R
#***********************************************************
# EXPERIMENTACIÓN EN AGRICULTURA
# Fernández Escobar, R.; Trapero, A.; Domínguez, J. 2010
# CAPÍTULO 13: ANÁLISIS DE LA VARIANZA COMBINADO
# Análisis de diferentes épocas (páginas 177 - 180)
#************************************************************
#### Importar Tabla 13.3
InviernoPrimavera <- read.csv("C:/Users/Administrator/Desktop/tabla 13.3.csv", header=TRUE)
attach(InviernoPrimavera)
print(InviernoPrimavera)## VARIEDAD EPOCA BLOQUE RENDIMIENTO
## 1 V1 Invierno I 0
## 2 V1 Invierno II 214
## 3 V1 Invierno III 425
## 4 V1 Invierno IV 40
## 5 V2 Invierno I 1252
## 6 V2 Invierno II 627
## 7 V2 Invierno III 716
## 8 V2 Invierno IV 1068
## 9 V3 Invierno I 2163
## 10 V3 Invierno II 2714
## 11 V3 Invierno III 2521
## 12 V3 Invierno IV 2240
## 13 V1 Primavera I 1036
## 14 V1 Primavera II 697
## 15 V1 Primavera III 849
## 16 V1 Primavera IV 1258
## 17 V2 Primavera I 1524
## 18 V2 Primavera II 1861
## 19 V2 Primavera III 2220
## 20 V2 Primavera IV 1744
## 21 V3 Primavera I 1312
## 22 V3 Primavera II 874
## 23 V3 Primavera III 695
## 24 V3 Primavera IV 1133#### Agregando función para calcular estadísticas descriptivas de interacciones
library(plyr)source("C:/Users/Administrator/Desktop/summarySE.r")
MEDIAS <- summarySE(InviernoPrimavera, measurevar="RENDIMIENTO", groupvars=c("VARIEDAD", "EPOCA"))
MEDIAS## VARIEDAD EPOCA N RENDIMIENTO sd se ci
## 1 V1 Invierno 4 169.75 193.8735 96.93673 308.4959
## 2 V1 Primavera 4 960.00 242.2602 121.13010 385.4900
## 3 V2 Invierno 4 915.75 294.1206 147.06029 468.0115
## 4 V2 Primavera 4 1837.25 290.9082 145.45410 462.8999
## 5 V3 Invierno 4 2409.50 254.7188 127.35940 405.3145
## 6 V3 Primavera 4 1003.50 273.1819 136.59093 434.6933#### Gráficos
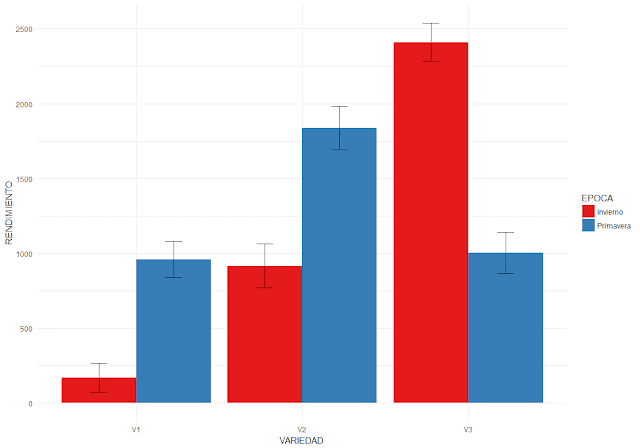
library(ggplot2)# Gráfico de barras errores típicos
ggplot(MEDIAS, aes(x = VARIEDAD,
y = RENDIMIENTO,
fill = EPOCA)) +
geom_bar(position = position_dodge(), stat = "identity") +
geom_errorbar(aes(ymin = RENDIMIENTO-se,
ymax = RENDIMIENTO+se),
width = .2,
position = position_dodge(.9)) +
scale_fill_brewer(palette = "Greens") + theme_minimal()#### Diagrama de dispersión
ggplot(InviernoPrimavera, aes(x=EPOCA, y=RENDIMIENTO, color=VARIEDAD)) +
geom_point(shape=1) + scale_color_brewer(palette = "Set1") +
geom_point(size = 3.0)#### Gráfico de lineas
ggplot(MEDIAS, aes(x = factor(EPOCA), y = RENDIMIENTO, colour = VARIEDAD, group = VARIEDAD)) +
scale_color_brewer(palette = "Set1") + geom_line(size = 1.0, linetype = 'solid')#### Gráfico de lineas + errores típicos
pd <- position_dodge(0.1) # mover barras de errores .05 hacia la izquierda y la derecha
SEgraph <- ggplot(data = MEDIAS, aes(x = EPOCA, y = RENDIMIENTO,
group = VARIEDAD,
color = VARIEDAD,
linetype = VARIEDAD,
shape = VARIEDAD)) +
geom_errorbar(aes(ymin = RENDIMIENTO-se, ymax = RENDIMIENTO+se),
width = .2, position = pd, size = 0.4, linetype = 'solid') +
geom_line(position = pd, size = 1.0, linetype = 'solid') +
geom_point(position = pd, size = 3.0) +
scale_color_brewer(palette = "Set1") + theme_minimal() +
ggtitle("Gráfico con errores típicos") +
xlab("EPOCA") + ylab("RENDIMIENTO(kg/ha)"); SEgraph#### Boxplot y líneas de interacción
library("plyr")
ipMEDIAS <- ddply(InviernoPrimavera,.(EPOCA,VARIEDAD), summarise, val = mean(RENDIMIENTO)) # precalculando medias
ggplot(InviernoPrimavera, aes(x = factor(EPOCA), y = RENDIMIENTO, colour = VARIEDAD)) +
geom_boxplot() + geom_point(data = ipMEDIAS, aes(y = val), position = position_dodge(width=0.75)) +
geom_line(data = ipMEDIAS, aes(y = val, group = VARIEDAD), position = position_dodge(width=0.75)) +
scale_x_discrete("Época") + scale_y_continuous("Rendimiento (kg/ha)") + theme_bw() + theme_bw() +
theme(axis.title.x = element_text(size = 12, hjust = 0.54, vjust = 0),
axis.title.y = element_text(size = 12, angle = 90, vjust = 0.25))#### Boxplot para interacciones
library(plotly)# EPOCA:VARIEDAD
gInvPrim <- plot_ly(InviernoPrimavera, y = ~RENDIMIENTO, color = ~EPOCA:VARIEDAD, type = "box",
boxpoints = "all", jitter = 0.3, pointpos = -1.8); gInvPrim# VARIEDAD:EPOCA
gInvPrim <- plot_ly(InviernoPrimavera, y = ~RENDIMIENTO, color = ~VARIEDAD:EPOCA, type = "box",
boxpoints = "all", jitter = 0.3, pointpos = -1.8); gInvPrim#### ANOVA para el rendimiento en Invierno
# Separando datos de Invierno
invierno <- InviernoPrimavera[1:12, ]; invierno## VARIEDAD EPOCA BLOQUE RENDIMIENTO
## 1 V1 Invierno I 0
## 2 V1 Invierno II 214
## 3 V1 Invierno III 425
## 4 V1 Invierno IV 40
## 5 V2 Invierno I 1252
## 6 V2 Invierno II 627
## 7 V2 Invierno III 716
## 8 V2 Invierno IV 1068
## 9 V3 Invierno I 2163
## 10 V3 Invierno II 2714
## 11 V3 Invierno III 2521
## 12 V3 Invierno IV 2240# Estadísticas descriptivas para VARIEDAD
library(doBy) ## Warning: package 'doBy' was built under R version 3.3.2library(pastecs)summaryBy(RENDIMIENTO ~ VARIEDAD, data = invierno, FUN = stat.desc)# Boxplot para rendimiento de variedades en invierno
gInvierno <- plot_ly(invierno, y = ~RENDIMIENTO, color = ~VARIEDAD, type = "box",
boxpoints = "all", jitter = 0.3, pointpos = -1.8); gInvierno# ANOVA Diseño en Bloques al Azar
ANOVAinvierno <- aov(RENDIMIENTO ~ BLOQUE + VARIEDAD, data = invierno)
summary(ANOVAinvierno)## Df Sum Sq Mean Sq F value Pr(>F)
## BLOQUE 3 19833 6611 0.073 0.972561
## VARIEDAD 2 10405714 5202857 57.060 0.000125 ***
## Residuals 6 547094 91182
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1#### ANOVA para el rendimiento en Primavera
# Separando datos de Primavera
primavera <- InviernoPrimavera[13:24, ]; primavera## VARIEDAD EPOCA BLOQUE RENDIMIENTO
## 13 V1 Primavera I 1036
## 14 V1 Primavera II 697
## 15 V1 Primavera III 849
## 16 V1 Primavera IV 1258
## 17 V2 Primavera I 1524
## 18 V2 Primavera II 1861
## 19 V2 Primavera III 2220
## 20 V2 Primavera IV 1744
## 21 V3 Primavera I 1312
## 22 V3 Primavera II 874
## 23 V3 Primavera III 695
## 24 V3 Primavera IV 1133# Estadísticas descriptivas para PRIMAVERA
summaryBy(RENDIMIENTO ~ VARIEDAD, data = primavera, FUN = stat.desc)# Boxplot para rendimiento de variedades en primavera
gPrimavera <- plot_ly(primavera, y = ~RENDIMIENTO, color = ~VARIEDAD, type = "box",
boxpoints = "all", jitter = 0.3, pointpos = -1.8); gPrimavera# ANOVA Diseño en Bloques al Azar
ANOVAinvierno <- aov(RENDIMIENTO ~ BLOQUE + VARIEDAD, data = primavera)
summary(ANOVAinvierno)## Df Sum Sq Mean Sq F value Pr(>F)
## BLOQUE 3 84709 28236 0.298 0.8262
## VARIEDAD 2 1955465 977733 10.308 0.0115 *
## Residuals 6 569129 94855
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1#### Modelo EPOCA EPOCA*REP(E) VARIEDAD VARIEDAD*EPOCA
# Opción 1
MODELO <- aov(RENDIMIENTO ~ EPOCA + Error(EPOCA/BLOQUE) + EPOCA*VARIEDAD, InviernoPrimavera)
summary(MODELO)# Opción 2
MODELO <- aov(RENDIMIENTO ~ EPOCA + EPOCA/BLOQUE + EPOCA*VARIEDAD, InviernoPrimavera)
summary(MODELO)## Df Sum Sq Mean Sq F value Pr(>F)
## EPOCA 1 62322 62322 0.670 0.429
## VARIEDAD 2 5522514 2761257 29.685 2.26e-05 ***
## EPOCA:BLOQUE 6 104542 17424 0.187 0.975
## EPOCA:VARIEDAD 2 6838665 3419332 36.760 7.63e-06 ***
## Residuals 12 1116223 93019
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1#### Descomposición de las sumas de cuadrados
#### de ambos factores en CONTRASTES ORTOGONALES,
#### con un grado de libertad
# Verificar niveles y orden de tratamientos
str(InviernoPrimavera)# Coeficientes de contraste
# Contraste V1 V2 V3;
# V3 vs. V1 + V2 VARIEDAD -1 -1 2;
# V1 + V2 VARIEDAD 1 -1 0;
# Crear matrix temporal
contrastmatrix <- cbind(c(-1, -1, 2),
c( 1, -1, 0)); contrastmatrix# Asignar matrix temporal a VARIEDAD
contrasts(InviernoPrimavera$VARIEDAD)<-contrastmatrix
InviernoPrimavera$VARIEDAD# Correr nuevamente el ANOVA con interacciones
CONTRASTAR <- aov(RENDIMIENTO ~ EPOCA + EPOCA/BLOQUE + EPOCA*VARIEDAD, InviernoPrimavera)
# Separar suma de cuadrados para VARIEDAD
summary(CONTRASTAR, split = list(VARIEDAD = list("V3 vs. V1 + V2" = 1,"V1 + V2" = 2)))## Df Sum Sq Mean Sq F value Pr(>F)
## EPOCA 1 62322 62322 0.670 0.429009
## VARIEDAD 2 5522514 2761257 29.685 2.26e-05 ***
## VARIEDAD: V3 vs. V1 + V2 1 2887574 2887574 31.043 0.000122 ***
## VARIEDAD: V1 + V2 1 2634941 2634941 28.327 0.000182 ***
## EPOCA:BLOQUE 6 104542 17424 0.187 0.974684
## EPOCA:VARIEDAD 2 6838665 3419332 36.760 7.63e-06 ***
## EPOCA:VARIEDAD: V3 vs. V1 + V2 1 6821438 6821438 73.334 1.86e-06 ***
## EPOCA:VARIEDAD: V1 + V2 1 17227 17227 0.185 0.674574
## Residuals 12 1116223 93019
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Códigos en SAS
/***********************************************************
EXPERIMENTACIÓN EN AGRICULTURA
Fernández
Escobar, R.; Trapero, A.; Domínguez, J. 2010
CAPÍTULO 13:
ANÁLISIS DE LA VARIANZA COMBINADO
Análisis de
diferentes épocas (páginas 177 - 180)
************************************************************/
DATA InviernoPrimavera;
INPUT VARIEDAD $ EPOCA $ BLOQUE $ RENDIMIENTO;
CARDS;
V1 Invierno I 0
V1 Invierno II 214
V1 Invierno III 425
V1 Invierno IV 40
V2 Invierno I 1252
V2 Invierno II 627
V2 Invierno III 716
V2 Invierno IV 1068
V3 Invierno I 2163
V3 Invierno II 2714
V3 Invierno III 2521
V3 Invierno IV 2240
V1 Primavera I 1036
V1 Primavera II 697
V1 Primavera III 849
V1 Primavera IV 1258
V2 Primavera I 1524
V2 Primavera II 1861
V2 Primavera III 2220
V2 Primavera IV 1744
V3 Primavera I 1312
V3 Primavera II 874
V3 Primavera III 695
V3 Primavera IV 1133
;
ODS HTML;
* Imprimiento datos completos: Invierno y Primavera;
PROC PRINT;
PROC MEANS MEAN STD STDERR MAXDEC=2;
VAR
RENDIMIENTO;
CLASS VARIEDAD EPOCA;
RUN;
*Ordenando y clasificando datos por VARIEDAD;
PROC SORT DATA =
InviernoPrimavera; BY VARIEDAD; RUN;
PROC UNIVARIATE DATA =
InviernoPrimavera; VAR RENDIMIENTO; BY VARIEDAD EPOCA;
RUN;
* Separando datos de Invierno;
DATA Invierno;
SET InviernoPrimavera(obs = 12); RUN; *Incluye las primeras 12 líneas;
PROC PRINT DATA=Invierno;
RUN;
* ANOVA Diseño Bloques al Azar: Datos de Invierno;
PROC GLM DATA =
Invierno;
CLASS VARIEDAD BLOQUE;
MODEL RENDIMIENTO = BLOQUE VARIEDAD;
RUN;
* Separando datos de Primavera;
DATA Primavera;
SET InviernoPrimavera(firstobs = 13); RUN; *Datos inician en línea 13;
PROC PRINT DATA=Primavera;
RUN;
* ANOVA Diseño Bloques al Azar: Datos de Primavera;
PROC GLM DATA =
Primavera;
CLASS VARIEDAD BLOQUE;
MODEL RENDIMIENTO = BLOQUE VARIEDAD;
RUN;
* Modelo EPOCA EPOCA*REP(E) VARIEDAD VARIEDAD*EPOCA
* Opción 1: ANOVA Combinado RENDIMIENTO (página
179);
PROC GLM DATA =
InviernoPrimavera;
CLASS VARIEDAD BLOQUE EPOCA;
MODEL RENDIMIENTO = EPOCA BLOQUE EPOCA*BLOQUE VARIEDAD
EPOCA*VARIEDAD;
RUN;
* Opción 2: ANOVA Combinado RENDIMIENTO (página 179)
Mejor!;
PROC MIXED DATA =
InviernoPrimavera METHOD = TYPE1;
CLASS VARIEDAD BLOQUE EPOCA;
MODEL RENDIMIENTO = EPOCA VARIEDAD EPOCA*VARIEDAD / DDFM=SATTERTH;
RANDOM EPOCA*BLOQUE;
RUN;
* Modelo EPOCA EPOCA*REP(E) VARIEDAD VARIEDAD*EPOCA
* Opción 1: ANOVA Combinado RENDIMIENTO (página
180);
PROC GLM DATA =
InviernoPrimavera;
CLASS VARIEDAD BLOQUE EPOCA;
MODEL RENDIMIENTO = EPOCA BLOQUE EPOCA*BLOQUE VARIEDAD
EPOCA*VARIEDAD / SOLUTION;
RANDOM EPOCA*BLOQUE / TEST;
*Contrastes ortogonales:
Variedades V1 V2
V3;
CONTRAST 'V3
vs. V1 + V2' VARIEDAD
-1
-1
2;
CONTRAST 'V1 vs. V2' VARIEDAD 1 -1 0;
*Época
* Variedad V1I V1P V2I V2P V3I V3P;
CONTRAST 'Época : (V3 vs. V1 + V2)' VARIEDAD*EPOCA
-1
1
-1
1
2
-2 ;
CONTRAST 'Época
: (V1 vs. V2)' VARIEDAD*EPOCA 1 -1 -1 1 0 0 ;
RUN;
* Opción 2: ANOVA
Combinado RENDIMIENTO (página 180) Mejor!;
PROC MIXED DATA =
InviernoPrimavera METHOD = TYPE1;
CLASS
VARIEDAD BLOQUE EPOCA;
MODEL
RENDIMIENTO = EPOCA VARIEDAD EPOCA*VARIEDAD / DDFM=SATTERTH;
RANDOM
EPOCA*BLOQUE;
*Contrastes ortogonales:
Variedades V1 V2
V3;
CONTRAST 'V3
vs. V1 + V2'
VARIEDAD -1 -1 2;
CONTRAST 'V1
+ V2' VARIEDAD 1 -1 0;
*Época * Variedad V1I V1P V2I V2P V3I V3P;
CONTRAST 'Época
: (V3 vs. V1 + V2)' VARIEDAD*EPOCA
-1 1 -1 1 2 -2 ;
CONTRAST 'Época
: (V1 vs. V2)'
VARIEDAD*EPOCA 1 -1 -1 1 0 0 ;
RUN;
QUIT;
ODS HTML CLOSE;
Datos : tabla 13.3.csv
R : capítulo 13c.R, summarySE.R
SAS : capítulo 13c.sas
No hay comentarios:
Publicar un comentario