Estudiando Agricultura en Taiwán: mayo 2017

Encontrarás explicación sobre selección de modelo en regresión con más de dos variables independientes en páginas 226 – 231, Experimentación en Agricultura.

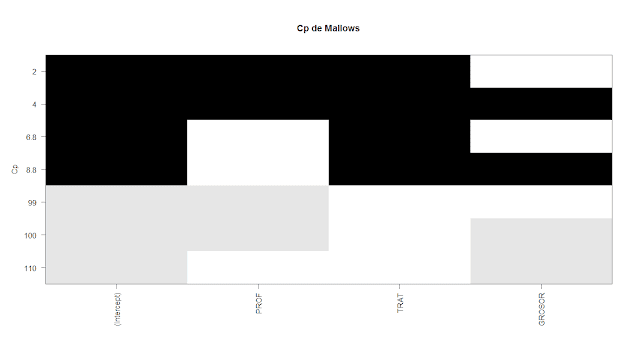plot(todos, scale = "Cp"   , main = "Cp de Mallows")

El Cp con el menor valor y el R²-ajustado con el mayor, sirven para seleccionar el modelo con las variables más apropiadas.

Códigos para el software R

#***********************************************************
# EXPERIMENTACIÓN EN AGRICULTURA                              
# Fernández Escobar, R.; Trapero, A.; Domínguez, J. 2010       
# CAPÍTULO 16: REGRESIÓN MÚLTIPLE
# REGRESIÓN CON MÁS DE DOS VARIABLES INDEPENDIENTES (pp. 226-231)
#************************************************************

#### Importar Tabla 16.2
SUELO <- read.csv("C:/Users/Administrator/Desktop/tabla 16.2.csv", header=TRUE)
attach(SUELO); knitr::kable(SUELO)

N_MINERAL	TRAT	GROSOR	PROF
26.34	0	0.5	20
28.25	0	0.5	30
26.24	0	0.5	50
37.28	0	0.5	70
42.04	0	0.5	90
21.15	0	1.0	20
34.38	0	1.0	30
26.67	0	1.0	50
28.39	0	1.0	70
40.50	0	1.0	90
35.53	0	2.0	20
22.30	0	2.0	30
20.75	0	2.0	50
20.35	0	2.0	70
47.32	0	2.0	90
44.75	1	0.5	20
74.16	1	0.5	30
62.11	1	0.5	50
57.41	1	0.5	70
60.78	1	0.5	90
41.54	1	1.0	20
61.10	1	1.0	30
63.67	1	1.0	50
62.31	1	1.0	70
65.21	1	1.0	90
51.80	1	2.0	20
74.04	1	2.0	30
60.69	1	2.0	50
56.52	1	2.0	70
69.23	1	2.0	90

#### El primer procedimiento: Best Subset Regression Models for N_MINERAL
library(leaps)

library(HH)

todos <- regsubsets(N_MINERAL ~ PROF + TRAT + GROSOR, data = SUELO, nbest=10)


# Posibles modelos representados por asteriscos
summary(todos); stars <- summary(todos); as.data.frame(stars$outmat)

## Subset selection object
## Call: regsubsets.formula(N_MINERAL ~ PROF + TRAT + GROSOR, data = SUELO, 
##     nbest = 10)
## 3 Variables  (and intercept)
##        Forced in Forced out
## PROF       FALSE      FALSE
## TRAT       FALSE      FALSE
## GROSOR     FALSE      FALSE
## 10 subsets of each size up to 3
## Selection Algorithm: exhaustive
##          PROF TRAT GROSOR
## 1  ( 1 ) " "  "*"  " "   
## 1  ( 2 ) "*"  " "  " "   
## 1  ( 3 ) " "  " "  "*"   
## 2  ( 1 ) "*"  "*"  " "   
## 2  ( 2 ) " "  "*"  "*"   
## 2  ( 3 ) "*"  " "  "*"   
## 3  ( 1 ) "*"  "*"  "*"

##          PROF TRAT GROSOR
## 1  ( 1 )         *       
## 1  ( 2 )    *            
## 1  ( 3 )                *
## 2  ( 1 )    *    *       
## 2  ( 2 )         *      *
## 2  ( 3 )    *           *
## 3  ( 1 )    *    *      *

# Opción 1
knitr::kable(summaryHH(todos))

model	p	rsq	rss	adjr2	cp	bic	stderr
T	2	0.7517322	2207.813	0.7428655	6.825148	-34.995022	8.879779
P	2	0.0515926	8434.064	0.0177209	99.395289	5.213262	17.355592
G	2	0.0000283	8892.618	-0.0356849	106.212940	6.801544	17.821154
P-T	3	0.8033248	1749.007	0.7887562	2.003748	-38.582452	8.048481
T-G	3	0.7517605	2207.561	0.7333724	8.821400	-31.597251	9.042208
P-G	3	0.0516209	8433.812	-0.0186294	101.391541	8.613563	17.673806
P-T-G	4	0.8033531	1748.755	0.7806631	4.000000	-35.185579	8.201208

# Opción 2, ordenados según página 228. No incluye el intercepto
knitr::kable(data.frame(summary(todos)$cp, summary(todos)$adjr2, summary(todos)$rsq, summary(todos)$rss))

summary.todos..cp	summary.todos..adjr2	summary.todos..rsq	summary.todos..rss
6.825148	0.7428655	0.7517322	2207.813
99.395289	0.0177209	0.0515926	8434.064
106.212940	-0.0356849	0.0000283	8892.618
2.003748	0.7887562	0.8033248	1749.007
8.821400	0.7333724	0.7517605	2207.561
101.391541	-0.0186294	0.0516209	8433.812
4.000000	0.7806631	0.8033531	1748.755

# Gráficos de diagnósticos de "Best Subset Regression Models for N_MINERAL"
plot(todos, scale = "r2"   , main = "Coeficiente de Determinación R^2")

plot(todos, scale = "Cp"   , main = "Cp de Mallows")

plot(todos, scale = "adjr2", main = "R^2 ajustado")

plot(todos, scale = "bic"  , main = "Criterio de información bayesiano (BIC)")

#### El segundo procedimiento
# Selección de "mejor" modelo, usando procedimientos "Forward" y "Backward"
# Opción 1
# Backward
modelo.completo <- lm(N_MINERAL ~ PROF + TRAT + GROSOR, data = SUELO) # regresión con todas las variables en SUELO
modelo.reducido <- step(modelo.completo, direction = "backward")

## Start:  AIC=129.96
## N_MINERAL ~ PROF + TRAT + GROSOR
## 
##          Df Sum of Sq    RSS    AIC
## - GROSOR  1       0.3 1749.0 127.97
## <none>                1748.8 129.96
## - PROF    1     458.8 2207.6 134.95
## - TRAT    1    6685.1 8433.8 175.16
## 
## Step:  AIC=127.97
## N_MINERAL ~ PROF + TRAT
## 
##        Df Sum of Sq    RSS    AIC
## <none>              1749.0 127.97
## - PROF  1     458.8 2207.8 132.96
## - TRAT  1    6685.1 8434.1 173.16

summary(modelo.reducido); modelo.reducido$anova

## 
## Call:
## lm(formula = N_MINERAL ~ PROF + TRAT, data = SUELO)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -13.9287  -4.8533  -0.0762   4.0864  17.1644 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 22.55961    3.63579   6.205 1.24e-06 ***
## PROF         0.15269    0.05737   2.661   0.0129 *  
## TRAT        29.85533    2.93889  10.159 1.01e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 8.048 on 27 degrees of freedom
## Multiple R-squared:  0.8033, Adjusted R-squared:  0.7888 
## F-statistic: 55.14 on 2 and 27 DF,  p-value: 2.922e-10

##       Step Df Deviance Resid. Df Resid. Dev      AIC
## 1          NA       NA        26   1748.755 129.9639
## 2 - GROSOR  1 0.252105        27   1749.007 127.9682

# Forward
modelo.fwd <- step(lm(N_MINERAL ~1), direction = "forward", scope = (~PROF + TRAT + GROSOR))

## Start:  AIC=172.75
## N_MINERAL ~ 1
## 
##          Df Sum of Sq    RSS    AIC
## + TRAT    1    6685.1 2207.8 132.96
## <none>                8892.9 172.75
## + PROF    1     458.8 8434.1 173.16
## + GROSOR  1       0.3 8892.6 174.75
## 
## Step:  AIC=132.96
## N_MINERAL ~ TRAT
## 
##          Df Sum of Sq    RSS    AIC
## + PROF    1    458.81 1749.0 127.97
## <none>                2207.8 132.96
## + GROSOR  1      0.25 2207.6 134.95
## 
## Step:  AIC=127.97
## N_MINERAL ~ TRAT + PROF
## 
##          Df Sum of Sq    RSS    AIC
## <none>                1749.0 127.97
## + GROSOR  1   0.25211 1748.8 129.96

summary(modelo.fwd); modelo.fwd$anova

## 
## Call:
## lm(formula = N_MINERAL ~ TRAT + PROF)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -13.9287  -4.8533  -0.0762   4.0864  17.1644 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 22.55961    3.63579   6.205 1.24e-06 ***
## TRAT        29.85533    2.93889  10.159 1.01e-10 ***
## PROF         0.15269    0.05737   2.661   0.0129 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 8.048 on 27 degrees of freedom
## Multiple R-squared:  0.8033, Adjusted R-squared:  0.7888 
## F-statistic: 55.14 on 2 and 27 DF,  p-value: 2.922e-10

##     Step Df  Deviance Resid. Df Resid. Dev      AIC
## 1        NA        NA        29   8892.870 172.7542
## 2 + TRAT -1 6685.0570        28   2207.813 132.9568
## 3 + PROF -1  458.8061        27   1749.007 127.9682

# Opción 2
# Usando Cp en regresión Stepwise
modelo.completo <- lm(N_MINERAL ~., data=SUELO)
MSE=(summary(modelo.completo)$sigma)^2 # guardar MSE para el modelo completo
intercepto <- lm(N_MINERAL~1) # regresión incluye solo la constante del intercepto
modelos <- step(intercepto, scope = list(upper = modelo.completo), scale = MSE); modelos

## Start:  AIC=104.22
## N_MINERAL ~ 1
## 
##          Df Sum of Sq    RSS       Cp
## + TRAT    1    6685.1 2207.8   6.8251
## + PROF    1     458.8 8434.1  99.3953
## <none>                8892.9 104.2167
## + GROSOR  1       0.3 8892.6 106.2129
## 
## Step:  AIC=6.83
## N_MINERAL ~ TRAT
## 
##          Df Sum of Sq    RSS       Cp
## + PROF    1     458.8 1749.0   2.0037
## <none>                2207.8   6.8251
## + GROSOR  1       0.3 2207.6   8.8214
## - TRAT    1    6685.1 8892.9 104.2167
## 
## Step:  AIC=2
## N_MINERAL ~ TRAT + PROF
## 
##          Df Sum of Sq    RSS      Cp
## <none>                1749.0  2.0037
## + GROSOR  1       0.3 1748.8  4.0000
## - PROF    1     458.8 2207.8  6.8251
## - TRAT    1    6685.1 8434.1 99.3953

## 
## Call:
## lm(formula = N_MINERAL ~ TRAT + PROF)
## 
## Coefficients:
## (Intercept)         TRAT         PROF  
##     22.5596      29.8553       0.1527

summary(modelos); modelos$anova

## 
## Call:
## lm(formula = N_MINERAL ~ TRAT + PROF)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -13.9287  -4.8533  -0.0762   4.0864  17.1644 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 22.55961    3.63579   6.205 1.24e-06 ***
## TRAT        29.85533    2.93889  10.159 1.01e-10 ***
## PROF         0.15269    0.05737   2.661   0.0129 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 8.048 on 27 degrees of freedom
## Multiple R-squared:  0.8033, Adjusted R-squared:  0.7888 
## F-statistic: 55.14 on 2 and 27 DF,  p-value: 2.922e-10

##     Step Df  Deviance Resid. Df Resid. Dev         Cp
## 1        NA        NA        29   8892.870 104.216688
## 2 + TRAT -1 6685.0570        28   2207.813   6.825148
## 3 + PROF -1  458.8061        27   1749.007   2.003748

#### Modelo final
modelo.final <- lm(N_MINERAL ~ PROF + TRAT, data = SUELO)
anova(modelo.final); summary(modelo.final)

## Analysis of Variance Table
## 
## Response: N_MINERAL
##           Df Sum Sq Mean Sq  F value    Pr(>F)    
## PROF       1  458.8   458.8   7.0827   0.01294 *  
## TRAT       1 6685.1  6685.1 103.1994 1.012e-10 ***
## Residuals 27 1749.0    64.8                       
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

## 
## Call:
## lm(formula = N_MINERAL ~ PROF + TRAT, data = SUELO)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -13.9287  -4.8533  -0.0762   4.0864  17.1644 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 22.55961    3.63579   6.205 1.24e-06 ***
## PROF         0.15269    0.05737   2.661   0.0129 *  
## TRAT        29.85533    2.93889  10.159 1.01e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 8.048 on 27 degrees of freedom
## Multiple R-squared:  0.8033, Adjusted R-squared:  0.7888 
## F-statistic: 55.14 on 2 and 27 DF,  p-value: 2.922e-10

#  Diagnósticos de modelo final
library(broom)

tidy(modelo.final); glance(modelo.final)

##          term  estimate  std.error statistic      p.value
## 1 (Intercept) 22.559610 3.63578542  6.204879 1.235274e-06
## 2        PROF  0.152687 0.05737219  2.661342 1.294477e-02
## 3        TRAT 29.855333 2.93888984 10.158711 1.011703e-10

##   r.squared adj.r.squared    sigma statistic      p.value df    logLik
## 1 0.8033248     0.7887562 8.048481  55.14108 2.921599e-10  3 -103.5523
##        AIC      BIC deviance df.residual
## 1 215.1045 220.7093 1749.007          27

knitr::kable(augment(modelo.final))

N_MINERAL	PROF	TRAT	.fitted	.se.fit	.resid	.hat	.sigma	.cooksd	.std.resid
26.34	20	0	25.61335	2.772923	0.7266504	0.1186992	8.200395	0.0004152	0.0961722
28.25	30	0	27.14022	2.431390	1.1097805	0.0912602	8.198621	0.0007004	0.1446450
26.24	50	0	30.19396	2.081274	-3.9539593	0.0668699	8.162422	0.0061782	-0.5085658
37.28	70	0	33.24770	2.320561	4.0323008	0.0831301	8.160113	0.0082737	0.5232209
42.04	90	0	36.30144	3.011903	5.7385610	0.1400407	8.111515	0.0320889	0.7688650
21.15	20	0	25.61335	2.772923	-4.4633496	0.1186992	8.148626	0.0156665	-0.5907244
34.38	30	0	27.14022	2.431390	7.2397805	0.0912602	8.065428	0.0298060	0.9436081
26.67	50	0	30.19396	2.081274	-3.5239593	0.0668699	8.170536	0.0049075	-0.4532584
28.39	70	0	33.24770	2.320561	-4.8576992	0.0831301	8.141231	0.0120076	-0.6303225
40.50	90	0	36.30144	3.011903	4.1985610	0.1400407	8.153595	0.0171771	0.5625324
35.53	20	0	25.61335	2.772923	9.9166504	0.1186992	7.935854	0.0773357	1.3124688
22.30	30	0	27.14022	2.431390	-4.8402195	0.0912602	8.141128	0.0133224	-0.6308576
20.75	50	0	30.19396	2.081274	-9.4439593	0.0668699	7.974545	0.0352456	-1.2147001
20.35	70	0	33.24770	2.320561	-12.8976992	0.0831301	7.764748	0.0846483	-1.6735722
47.32	90	0	36.30144	3.011903	11.0185610	0.1400407	7.863811	0.1183039	1.4762910
44.75	20	1	55.46868	2.772923	-10.7186829	0.1186992	7.890216	0.0903510	-1.4186178
74.16	30	1	56.99555	2.431390	17.1644472	0.0912602	7.402708	0.1675377	2.2371551
62.11	50	1	60.04929	2.081274	2.0607073	0.0668699	8.191122	0.0016781	0.2650521
57.41	70	1	63.10303	2.320561	-5.6930325	0.0831301	8.118493	0.0164923	-0.7387132
60.78	90	1	66.15677	3.011903	-5.3767724	0.1400407	8.122594	0.0281704	-0.7203918
41.54	20	1	55.46868	2.772923	-13.9286829	0.1186992	7.668289	0.1525704	-1.8434613
61.10	30	1	56.99555	2.431390	4.1044472	0.0912602	8.158217	0.0095799	0.5349596
63.67	50	1	60.04929	2.081274	3.6207073	0.0668699	8.168792	0.0051806	0.4657023
62.31	70	1	63.10303	2.320561	-0.7930325	0.0831301	8.200191	0.0003200	-0.1029019
65.21	90	1	66.15677	3.011903	-0.9467724	0.1400407	8.199355	0.0008735	-0.1268506
51.80	20	1	55.46868	2.772923	-3.6686829	0.1186992	8.165913	0.0105845	-0.4855502
74.04	30	1	56.99555	2.431390	17.0444472	0.0912602	7.414434	0.1652033	2.2215147
60.69	50	1	60.04929	2.081274	0.6407073	0.0668699	8.200768	0.0001622	0.0824090
56.52	70	1	63.10303	2.320561	-6.5830325	0.0831301	8.090217	0.0220519	-0.8541973
69.23	90	1	66.15677	3.011903	3.0732276	0.1400407	8.176008	0.0092032	0.4117578

# Intervalo de confianza (95%) y predicción
intervalo  <- predict(modelo.final, interval = "confidence")
prediccion <- predict(modelo.final, interval = "prediction")

knitr::kable(data.frame(N_MINERAL, intervalo, prediccion))

N_MINERAL	fit	lwr	upr	fit.1	lwr.1	upr.1
26.34	25.61335	19.92378	31.30292	25.61335	8.146600	43.08010
28.25	27.14022	22.15142	32.12902	27.14022	9.889009	44.39143
26.24	30.19396	25.92354	34.46438	30.19396	13.136625	47.25129
37.28	33.24770	28.48630	38.00910	33.24770	16.060871	50.43453
42.04	36.30144	30.12152	42.48135	36.30144	18.668870	53.93401
21.15	25.61335	19.92378	31.30292	25.61335	8.146600	43.08010
34.38	27.14022	22.15142	32.12902	27.14022	9.889009	44.39143
26.67	30.19396	25.92354	34.46438	30.19396	13.136625	47.25129
28.39	33.24770	28.48630	38.00910	33.24770	16.060871	50.43453
40.50	36.30144	30.12152	42.48135	36.30144	18.668870	53.93401
35.53	25.61335	19.92378	31.30292	25.61335	8.146600	43.08010
22.30	27.14022	22.15142	32.12902	27.14022	9.889009	44.39143
20.75	30.19396	25.92354	34.46438	30.19396	13.136625	47.25129
20.35	33.24770	28.48630	38.00910	33.24770	16.060871	50.43453
47.32	36.30144	30.12152	42.48135	36.30144	18.668870	53.93401
44.75	55.46868	49.77911	61.15825	55.46868	38.001934	72.93543
74.16	56.99555	52.00675	61.98435	56.99555	39.744342	74.24676
62.11	60.04929	55.77887	64.31972	60.04929	42.991959	77.10663
57.41	63.10303	58.34163	67.86443	63.10303	45.916204	80.28986
60.78	66.15677	59.97686	72.33669	66.15677	48.524203	83.78934
41.54	55.46868	49.77911	61.15825	55.46868	38.001934	72.93543
61.10	56.99555	52.00675	61.98435	56.99555	39.744342	74.24676
63.67	60.04929	55.77887	64.31972	60.04929	42.991959	77.10663
62.31	63.10303	58.34163	67.86443	63.10303	45.916204	80.28986
65.21	66.15677	59.97686	72.33669	66.15677	48.524203	83.78934
51.80	55.46868	49.77911	61.15825	55.46868	38.001934	72.93543
74.04	56.99555	52.00675	61.98435	56.99555	39.744342	74.24676
60.69	60.04929	55.77887	64.31972	60.04929	42.991959	77.10663
56.52	63.10303	58.34163	67.86443	63.10303	45.916204	80.28986
69.23	66.15677	59.97686	72.33669	66.15677	48.524203	83.78934

# Gráficos de diagnósticos
par(mfrow = c(1, 1))
plot(modelo.final, 1) # Residuos vs. Estimados

plot(modelo.final, 2) # Normal Q-Q

plot(modelo.final, 3) # Residuos estandarizados vs Estimados

plot(modelo.final, 4) # Cook's distance

plot(modelo.final, 5) # Residuos vs. leverage

plot(modelo.final, 6) # Cook's distance vs. leverage

Códigos para el software SAS

/***********************************************************

EXPERIMENTACIÓN EN AGRICULTURA

Fernández Escobar, R.; Trapero, A.; Domínguez, J. 2010

CAPÍTULO 16: REGRESIÓN MÚLTIPLE

REGRESIÓN CON MÁS DE DOS VARIABLES INDEPENDIENTES (pp. 226-231)

************************************************************/

DATA SUELO;

INPUT N_MINERAL TRAT GROSOR PROF;

LABEL

N_MINERAL= "mg N/kg suelo"

TRAT = "kg N/árbol"

GROSOR = "mm"

PROF = "cm";

CARDS;

26.34 0 0.5 20

28.25 0 0.5 30

26.24 0 0.5 50

37.28 0 0.5 70

42.04 0 0.5 90

21.15 0 1 20

34.38 0 1 30

26.67 0 1 50

28.39 0 1 70

40.5 0 1 90

35.53 0 2 20

22.3 0 2 30

20.75 0 2 50

20.35 0 2 70

47.32 0 2 90

44.75 1 0.5 20

74.16 1 0.5 30

62.11 1 0.5 50

57.41 1 0.5 70

60.78 1 0.5 90

41.54 1 1 20

61.1 1 1 30

63.67 1 1 50

62.31 1 1 70

65.21 1 1 90

51.8 1 2 20

74.04 1 2 30

60.69 1 2 50

56.52 1 2 70

69.23 1 2 90

;

ODS HTML;

* Mostrar datos a analizar;

PROC PRINT DATA = SUELO;

RUN;

* El primer procedimiento: Best Subset Regression Models;

PROC REG;

MODEL N_MINERAL = PROF TRAT GROSOR / SELECTION = CP ADJRSQ RSQUARE PRESS MSE SSE SBC SP PC B BIC AIC JP;

RUN;

* El segundo procedimiento: Stepwise Linear Regression;

PROC REG;

MODEL N_MINERAL = PROF TRAT GROSOR / SELECTION = STEPWISE;

RUN;

* Regresión múltiple;

PROC REG;

MODEL N_MINERAL = PROF TRAT / R P CLM CLI influence;

RUN;

* Correlación;

PROC CORR PEARSON;

VAR N_MINERAL PROF TRAT GROSOR; *Valor de Correlación Múltiple es tan grande como el mayor de los coeficientes simples;

RUN;

* Correlación Parcial;

PROC CORR;

VAR GROSOR;

WITH N_MINERAL;

PARTIAL PROF TRAT;

RUN;

QUIT;

ODS HTML CLOSE;

------------------------------------------------------------

Archivos adjuntos:

capítulo16b.r, tabla 16.2.csv, capítulo 16b.sas

Estudiando Agricultura en Taiwán

Páginas

mayo 31, 2017

Lichi (6) — corte transversal

mayo 30, 2017

Regresión múltiple