Estudiando Agricultura en Taiwán: ANOVA combinado (1)

El Capítulo 13, “Análisis de Varianza Combinado”, en Experimentación en Agricultura, junta varios análisis descritos en secciones previas.

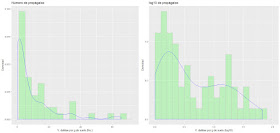A la izquierda, número de propágalos cuantificados durante muestreo (no.); a la derecha, números del muestreo transformados con log10(no. + 1).

También, da una excelente exposición sobre análisis e interpretación de datos recopilados periódicamente, ej. Respuesta, en altura de planta a aplicaciones de fertilizantes; ganancia de peso en cerdos alimentados con diferentes dietas. Datos que cómodamente son recolectados diaria-, semanal-, o mensualmente, con intervalos sucesivos, desde el inicio hasta el final del experimento.

# Box-plot (opción 2)
#### Box-and-Whisker con puntos para inspeccionar valores atípicos
dotplot1 <- ggplot(data = datosT, aes(x = TRAT, y = PROP)) +
  ggtitle("V. dahliae por g de suelo (No.)") +
  xlab("Tratamientos de suelo") + ylab("Número de propágalos") +
  geom_point(position = position_jitter(height = 0.2, width = 0.2), size = 2) +
  geom_boxplot(alpha = 0.1)

dotplot2 <- ggplot(data = datosT, aes(x = TRAT, y = LOPROP)) +
  ggtitle("V. dahliae por g de suelo (log10)") +
  xlab("Tratamientos de suelo") + ylab("log10 de propágalos") +
  geom_point(position = position_jitter(height = 0.2, width = 0.2), size = 2) +
  geom_boxplot(alpha = 0.1)

Para aliviar sobrecarga de códigos, rebanamos el Capítulo en 5 entregas: ANOVA combinado (1) — un muestreo; ANOVA combinado (2) — mediciones temporales repetidas; ANOVA combinado (3) — diferentes épocas-años; ANOVA combinado (4) — diferentes localidades; ANOVA combinado (5) — experimento de larga duración.

# #### gráficos iniciales
library(DescTools); Desc(datosT, plot = T)

En los siguientes códigos, ofrecemos opciones para representar y calcular el mismo gráfico o resultado. Lo hacemos para archivar la plétora de alternativas existentes.

Códigos en R

#***********************************************************
# EXPERIMENTACIÓN EN AGRICULTURA                              
# Fernández Escobar, R.; Trapero, A.; Domínguez, J. 2010       
# CAPÍTULO 13: ANÁLISIS DE LA VARIANZA COMBINADO 
# (páginas 167 - 172) 
#************************************************************

# Importar datos
datos <- read.csv("C:/Users/Administrator/Desktop/tabla 13.1.csv", header=TRUE)
attach(datos); datos

#### Crear y etiquetar variables en datos "Propágalos"
# tratamientos etiquetados
TRAT <- factor(TRAT, levels = c(0,1,2), labels = c("Sin solarizar", "Solarizado 1", "Solarizado 2"))
REP  <- factor(REP)
MUES <- factor(MUES)
datosID  <- data.frame(TRAT, REP, MUES, PROP); datosID

# transformación a log base 10
LOPROP <- log10(PROP+1)
datosT <- data.frame(datosID, LOPROP); datosT

##             TRAT REP MUES PROP     LOPROP
## 1  Sin solarizar   1    1 18.4 1.28780173
## 2  Sin solarizar   1    2 19.8 1.31806333
## 3  Sin solarizar   1    3 23.6 1.39093511
## 4  Sin solarizar   1    4 60.2 1.78675142
## 5  Sin solarizar   1    5 34.5 1.55022835
## 6  Sin solarizar   1    6 15.7 1.22271647
## 7  Sin solarizar   2    1 28.3 1.46686762
## 8  Sin solarizar   2    2 65.4 1.82216808
## 9  Sin solarizar   2    3 23.1 1.38201704
## 10 Sin solarizar   2    4 34.5 1.55022835
## 11 Sin solarizar   2    5  9.6 1.02530587
## 12 Sin solarizar   2    6 16.4 1.24054925
## 13 Sin solarizar   3    1 13.4 1.15836249
## 14 Sin solarizar   3    2 12.0 1.11394335
## 15 Sin solarizar   3    3  7.1 0.90848502
## 16 Sin solarizar   3    4 15.0 1.20411998
## 17 Sin solarizar   3    5  9.6 1.02530587
## 18 Sin solarizar   3    6 45.3 1.66558099
## 19 Sin solarizar   4    1 16.5 1.24303805
## 20 Sin solarizar   4    2  8.1 0.95904139
## 21 Sin solarizar   4    3 12.7 1.13672057
## 22 Sin solarizar   4    4 15.8 1.22530928
## 23 Sin solarizar   4    5  6.6 0.88081359
## 24 Sin solarizar   4    6 33.2 1.53402611
## 25  Solarizado 1   1    1  0.6 0.20411998
## 26  Solarizado 1   1    2  1.5 0.39794001
## 27  Solarizado 1   1    3  1.1 0.32221929
## 28  Solarizado 1   1    4  6.2 0.85733250
## 29  Solarizado 1   1    5  0.5 0.17609126
## 30  Solarizado 1   1    6  0.2 0.07918125
## 31  Solarizado 1   2    1  0.7 0.23044892
## 32  Solarizado 1   2    2  2.7 0.56820172
## 33  Solarizado 1   2    3  1.2 0.34242268
## 34  Solarizado 1   2    4  4.4 0.73239376
## 35  Solarizado 1   2    5  7.3 0.91907809
## 36  Solarizado 1   2    6  0.5 0.17609126
## 37  Solarizado 1   3    1  7.0 0.90308999
## 38  Solarizado 1   3    2  3.6 0.66275783
## 39  Solarizado 1   3    3  0.8 0.25527251
## 40  Solarizado 1   3    4  0.5 0.17609126
## 41  Solarizado 1   3    5  1.2 0.34242268
## 42  Solarizado 1   3    6  0.9 0.27875360
## 43  Solarizado 1   4    1  2.3 0.51851394
## 44  Solarizado 1   4    2  0.8 0.25527251
## 45  Solarizado 1   4    3  3.7 0.67209786
## 46  Solarizado 1   4    4  1.9 0.46239800
## 47  Solarizado 1   4    5  6.5 0.87506126
## 48  Solarizado 1   4    6  1.5 0.39794001
## 49  Solarizado 2   1    1  2.8 0.57978360
## 50  Solarizado 2   1    2  1.2 0.34242268
## 51  Solarizado 2   1    3  0.6 0.20411998
## 52  Solarizado 2   1    4  0.9 0.27875360
## 53  Solarizado 2   1    5  0.0 0.00000000
## 54  Solarizado 2   1    6  0.3 0.11394335
## 55  Solarizado 2   2    1  0.0 0.00000000
## 56  Solarizado 2   2    2  0.2 0.07918125
## 57  Solarizado 2   2    3  0.4 0.14612804
## 58  Solarizado 2   2    4  2.6 0.55630250
## 59  Solarizado 2   2    5  0.3 0.11394335
## 60  Solarizado 2   2    6  0.5 0.17609126
## 61  Solarizado 2   3    1  1.0 0.30103000
## 62  Solarizado 2   3    2  2.7 0.56820172
## 63  Solarizado 2   3    3  1.8 0.44715803
## 64  Solarizado 2   3    4  0.5 0.17609126
## 65  Solarizado 2   3    5  0.0 0.00000000
## 66  Solarizado 2   3    6  0.8 0.25527251
## 67  Solarizado 2   4    1  0.5 0.17609126
## 68  Solarizado 2   4    2  1.6 0.41497335
## 69  Solarizado 2   4    3  0.4 0.14612804
## 70  Solarizado 2   4    4  0.2 0.07918125
## 71  Solarizado 2   4    5  0.2 0.07918125
## 72  Solarizado 2   4    6  0.0 0.00000000

attach(datosT)

#### Estadística Descriptiva y Gráficos
source("C:/Users/Administrator/Desktop/summarySE.r") # Función summarySE

# sin transformar
summarySE(datosT, measurevar = "PROP", groupvars = c("TRAT", "REP"))

##             TRAT REP N       PROP         sd        se         ci
## 1  Sin solarizar   1 6 28.7000000 16.7702117 6.8464103 17.5992578
## 2  Sin solarizar   2 6 29.5500000 19.6153766 8.0079440 20.5850753
## 3  Sin solarizar   3 6 17.0666667 14.1109414 5.7607677 14.8085248
## 4  Sin solarizar   4 6 15.4833333  9.5518410 3.8995228 10.0240424
## 5   Solarizado 1   1 6  1.6833333  2.2604572 0.9228278  2.3722043
## 6   Solarizado 1   2 6  2.8000000  2.6487733 1.0813572  2.7797171
## 7   Solarizado 1   3 6  2.3333333  2.5468935 1.0397649  2.6728008
## 8   Solarizado 1   4 6  2.7833333  2.0614720 0.8415924  2.1633822
## 9   Solarizado 2   1 6  0.9666667  0.9933110 0.4055175  1.0424159
## 10  Solarizado 2   2 6  0.6666667  0.9626353 0.3929942  1.0102238
## 11  Solarizado 2   3 6  1.1333333  0.9709102 0.3963724  1.0189078
## 12  Solarizado 2   4 6  0.4833333  0.5741661 0.2344023  0.6025503

summarySE(datosT, measurevar = "PROP", groupvars = c("TRAT"))

##            TRAT  N    PROP         sd        se        ci
## 1 Sin solarizar 24 22.7000 15.8556258 3.2365161 6.6952436
## 2  Solarizado 1 24  2.4000  2.2771072 0.4648126 0.9615381
## 3  Solarizado 2 24  0.8125  0.8714368 0.1778813 0.3679755

# transformados
summarySE(datosT, measurevar = "LOPROP", groupvars = c("TRAT", "REP"))

##             TRAT REP N    LOPROP        sd         se        ci
## 1  Sin solarizar   1 6 1.4260827 0.2092257 0.08541605 0.2195690
## 2  Sin solarizar   2 6 1.4145227 0.2720823 0.11107713 0.2855329
## 3  Sin solarizar   3 6 1.1792996 0.2603267 0.10627795 0.2731962
## 4  Sin solarizar   4 6 1.1631582 0.2323220 0.09484508 0.2438070
## 5   Solarizado 1   1 6 0.3394807 0.2773663 0.11323432 0.2910781
## 6   Solarizado 1   2 6 0.4947727 0.2954746 0.12062699 0.3100815
## 7   Solarizado 1   3 6 0.4363980 0.2840033 0.11594386 0.2980432
## 8   Solarizado 1   4 6 0.5302139 0.2176584 0.08885865 0.2284184
## 9   Solarizado 2   1 6 0.2531705 0.2005901 0.08189058 0.2105064
## 10  Solarizado 2   2 6 0.1786077 0.1947729 0.07951571 0.2044016
## 11  Solarizado 2   3 6 0.2912923 0.2002437 0.08174915 0.2101429
## 12  Solarizado 2   4 6 0.1492592 0.1438290 0.05871795 0.1509393

summarySE(datosT, measurevar = "LOPROP", groupvars = c("TRAT"))

##            TRAT  N    LOPROP        sd         se         ci
## 1 Sin solarizar 24 1.2957658 0.2613633 0.05335056 0.11036404
## 2  Solarizado 1 24 0.4502163 0.2626273 0.05360857 0.11089777
## 3  Solarizado 2 24 0.2180824 0.1832201 0.03739964 0.07736704

# #### gráficos iniciales
library(DescTools)

Desc(datosT, plot = T)

## Describe datosT (data.frame):
## 1 - TRAT (factor)
## 
##   length      n    NAs unique levels  dupes
##    7e+01  7e+01      0  3e+00  3e+00      y
##          100.0%   0.0%                     
## 
##            level   freq   perc  cumfreq  cumperc
## 1  Sin solarizar  2e+01  33.3%    2e+01    33.3%
## 2   Solarizado 1  2e+01  33.3%    5e+01    66.7%
## 3   Solarizado 2  2e+01  33.3%    7e+01   100.0%

#### Gráficos con más detalles
library(lattice)
library(car)

library(agricolae)

with(datosT, xyplot(LOPROP ~ TRAT ))

with(datosT, xyplot(LOPROP ~ TRAT | REP ))

with(datosT, xyplot(LOPROP ~ TRAT | MUES))

with(datosT, xyplot(LOPROP ~ MUES | TRAT))

with(datosT, xyplot(LOPROP ~ REP  | TRAT))

with(datosT, xyplot(LOPROP ~ TRAT | REP , groups = MUES))

with(datosT, xyplot(LOPROP ~ REP  | TRAT, groups = MUES))

with(datosT, xyplot(LOPROP ~ TRAT | MUES, groups = REP ))

with(datosT, xyplot(LOPROP ~ MUES | TRAT, groups = REP ))

with(datosT, xyplot(LOPROP ~ REP  | MUES, groups = TRAT ))

with(datosT, xyplot(LOPROP ~ MUES | REP , groups = TRAT ))

with(datosT, xyplot(LOPROP ~ TRAT | REP , groups = MUES , aspect = "xy"))

with(datosT, xyplot(LOPROP ~ REP  | TRAT, groups = MUES , aspect = "xy"))

with(datosT, xyplot(LOPROP ~ TRAT | MUES, groups = REP  , aspect = "xy"))

with(datosT, xyplot(LOPROP ~ MUES | TRAT, groups = REP  , aspect = "xy"))

with(datosT, xyplot(LOPROP ~ REP  | MUES, groups = TRAT , aspect = "xy"))

with(datosT, xyplot(LOPROP ~ MUES | REP , groups = TRAT , aspect = "xy"))

with(datosT, xyplot(LOPROP ~ TRAT | REP , groups = MUES , aspect = "xy", type = "o"))

with(datosT, xyplot(LOPROP ~ REP  | TRAT, groups = MUES , aspect = "xy", type = "o"))

with(datosT, xyplot(LOPROP ~ TRAT | MUES, groups = REP  , aspect = "xy", type = "o"))

with(datosT, xyplot(LOPROP ~ MUES | TRAT, groups = REP  , aspect = "xy", type = "o"))

with(datosT, xyplot(LOPROP ~ REP  | MUES, groups = TRAT , aspect = "xy", type = "o"))

with(datosT, xyplot(LOPROP ~ MUES | REP , groups = TRAT , aspect = "xy", type = "o"))

with(datosT, xyplot(LOPROP ~ TRAT | REP , groups = MUES , aspect = "xy", type = "a"))

with(datosT, xyplot(LOPROP ~ REP  | TRAT, groups = MUES , aspect = "xy", type = "a"))

with(datosT, xyplot(LOPROP ~ TRAT | MUES, groups = REP  , aspect = "xy", type = "a"))

with(datosT, xyplot(LOPROP ~ MUES | TRAT, groups = REP  , aspect = "xy", type = "a"))

with(datosT, xyplot(LOPROP ~ REP  | MUES, groups = TRAT , aspect = "xy", type = "a"))

with(datosT, xyplot(LOPROP ~ MUES | REP , groups = TRAT , aspect = "xy", type = "a"))

histogram(~LOPROP | interaction(TRAT, REP), data = datosT)

histogram(~LOPROP | interaction(TRAT, MUES), data = datosT)

library (ggplot2)

# Histogramas + densidades (opción 1)
par(mfrow = c(1,2))
hist(PROP, prob = TRUE, col = "grey")  # datos sin transformar
lines(density(PROP),    col = "blue", lwd = 2) 
lines(density(PROP , adjust = 2), lty = "dotted", col = "darkgreen", lwd = 2) 

hist(LOPROP, prob = TRUE, col = "grey") # datos transformados
lines(density(LOPROP),    col = "blue", lwd = 2)
lines(density(LOPROP , adjust = 2), lty = "dotted", col = "darkgreen", lwd = 2)

# Histogramas + densidades (opción 2)
plot1 <- ggplot(data   = datosT, aes(PROP)) + #  datos no transformados
  geom_histogram(aes(y = ..density..), breaks=seq(1, 75, by=4), col="grey", fill="green", alpha=.2) + 
  geom_density(col     = 4) + labs(title = "Número de propágalos") + 
  labs(x = "V. dahliae por g de suelo (No.)", y = "Densidad")

plot2 <- ggplot(data   = datosT, aes(LOPROP)) + # datos transformados
  geom_histogram(aes(y = ..density..), breaks=seq(0, 2, by=.1), col="grey", fill="green", alpha=.2) + 
  geom_density(col     = 4) + labs(title = "log10 de propágalos") + 
  labs(x = "V. dahliae por g de suelo (log10)", y = "Densidad")

# mostar gráficos juntos
library(gridExtra)

grid.arrange(plot1, plot2, nrow=1, ncol=2)

#### Gráficos Box and Whisker
# Box-plot (opción 1)
library(HH)

BW1 <- bwplot(PROP ~ TRAT, data = datosT, scales=list(cex=1.5),
       ylab=list("Número de propágalos", cex = 1.5),
       xlab=list("Tratamientos de suelo",cex = 1.5)); BW1

BW2 <- bwplot(LOPROP ~ TRAT, data = datosT, scales=list(cex=1.5), 
       ylab = list("log10, datos transformados", cex=1.5),
       xlab=list("Tratamientos de suelo",cex=1.5)); BW2

# Box-plot (opción 2)
#### Box-and-Whisker con puntos para inspeccionar valores atípicos
dotplot1 <- ggplot(data = datosT, aes(x = TRAT, y = PROP)) +
  ggtitle("V. dahliae por g de suelo (No.)") +
  xlab("Tratamientos de suelo") + ylab("Número de propágalos") +
  geom_point(position = position_jitter(height = 0.2, width = 0.2), size = 2) +
  geom_boxplot(alpha = 0.1)

dotplot2 <- ggplot(data = datosT, aes(x = TRAT, y = LOPROP)) +
  ggtitle("V. dahliae por g de suelo (log10)") +
  xlab("Tratamientos de suelo") + ylab("log10 de propágalos") +
  geom_point(position = position_jitter(height = 0.2, width = 0.2), size = 2) +
  geom_boxplot(alpha = 0.1)

# agrupando gráficos
grid.arrange(dotplot1, dotplot2, nrow=1, ncol=2)

#### Box-plot TRAT*REP (opción 3)
par(mfrow = c(1,1))
boxplot(PROP   ~ TRAT*REP, col = c("green", "red", "blue"), datosT) # sin transformar

boxplot(LOPROP ~ TRAT*REP, col = c("green", "red", "blue"), datosT) # transformados

#### ANOVA combinados
# Ejemplo de un ANOVA con un muestreo (pp. 169)
modelo1 <- aov(LOPROP ~ TRAT * REP + Error(TRAT + REP), datosT); summary(modelo1)

## Error: TRAT
##      Df Sum Sq Mean Sq
## TRAT  2  15.44   7.721
## 
## Error: REP
##     Df  Sum Sq Mean Sq
## REP  3 0.07266 0.02422
## 
## Error: Within
##           Df Sum Sq Mean Sq F value Pr(>F)
## TRAT:REP   6  0.503 0.08385     1.5  0.194
## Residuals 60  3.354 0.05590

library(nlme) # únicamente para determinar SS total

anova(glm(LOPROP ~ TRAT * REP, family = gaussian(link = identity)), test = "F")

## Analysis of Deviance Table
## 
## Model: gaussian, link: identity
## 
## Response: LOPROP
## 
## Terms added sequentially (first to last)
## 
## 
##          Df Deviance Resid. Df Resid. Dev        F Pr(>F)    
## NULL                        71    19.3716                    
## TRAT      2  15.4419        69     3.9296 138.1261 <2e-16 ***
## REP       3   0.0727        66     3.8570   0.4333 0.7300    
## TRAT:REP  6   0.5031        60     3.3539   1.5000 0.1937    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

#### El nuevo ANOVA (empleando diferentes códigos para el mismo propósito)
modelo2a <- aov(lm(LOPROP ~ TRAT + REP)); modelo2a

## Call:
##    aov(formula = lm(LOPROP ~ TRAT + REP))
## 
## Terms:
##                      TRAT       REP Residuals
## Sum of Squares  15.441932  0.072657  3.856973
## Deg. of Freedom         2         3        66
## 
## Residual standard error: 0.2417416
## Estimated effects may be unbalanced

modelo2b <- aov(LOPROP ~ TRAT + REP); summary(modelo2b)

##             Df Sum Sq Mean Sq F value Pr(>F)    
## TRAT         2 15.442   7.721 132.120 <2e-16 ***
## REP          3  0.073   0.024   0.414  0.743    
## Residuals   66  3.857   0.058                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

modelo2c <- anova(glm(LOPROP ~ TRAT + REP, family = gaussian(link = identity)), test = "F");modelo2c

## Analysis of Deviance Table
## 
## Model: gaussian, link: identity
## 
## Response: LOPROP
## 
## Terms added sequentially (first to last)
## 
## 
##      Df Deviance Resid. Df Resid. Dev        F Pr(>F)    
## NULL                    71    19.3716                    
## TRAT  2  15.4419        69     3.9296 132.1201 <2e-16 ***
## REP   3   0.0727        66     3.8570   0.4144 0.7432    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

boxplot(LOPROP ~ TRAT,datosT)

plot(modelo2a)

library(car)
modelo3 <- lm(LOPROP ~ TRAT + REP)
Anova(modelo3, type = 'III')

## Anova Table (Type III tests)
## 
## Response: LOPROP
##              Sum Sq Df  F value Pr(>F)    
## (Intercept) 20.7188  1 354.5374 <2e-16 ***
## TRAT        15.4419  2 132.1201 <2e-16 ***
## REP          0.0727  3   0.4144 0.7432    
## Residuals    3.8570 66                    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

#### Contrastes ortogonales
# coeficientes de TRAT
str(datosT)

## 'data.frame':    72 obs. of  5 variables:
##  $ TRAT  : Factor w/ 3 levels "Sin solarizar",..: 1 1 1 1 1 1 1 1 1 1 ...
##  $ REP   : Factor w/ 4 levels "1","2","3","4": 1 1 1 1 1 1 2 2 2 2 ...
##  $ MUES  : Factor w/ 6 levels "1","2","3","4",..: 1 2 3 4 5 6 1 2 3 4 ...
##  $ PROP  : num  18.4 19.8 23.6 60.2 34.5 15.7 28.3 65.4 23.1 34.5 ...
##  $ LOPROP: num  1.29 1.32 1.39 1.79 1.55 ...

c1 <- c(2,-1, -1)
c2 <- c(0, 1, -1)
# crear una matrix temporal
mat.temp <- rbind(constant = 1/3, c1, c2); mat.temp

##               [,1]       [,2]       [,3]
## constant 0.3333333  0.3333333  0.3333333
## c1       2.0000000 -1.0000000 -1.0000000
## c2       0.0000000  1.0000000 -1.0000000

# obtiener matrix inversa
mat <- solve(mat.temp); mat

##      constant         c1   c2
## [1,]        1  0.3333333  0.0
## [2,]        1 -0.1666667  0.5
## [3,]        1 -0.1666667 -0.5

# eliminar la primera columna de la matrix
mat <- mat[ , -1]; mat

##              c1   c2
## [1,]  0.3333333  0.0
## [2,] -0.1666667  0.5
## [3,] -0.1666667 -0.5

# cálculo de contrast (opción 1)
modelo5 <- lm(LOPROP ~ TRAT, data = datosT, 
              contrasts = list(TRAT = mat)); summary(modelo5)

## Call:
## lm(formula = LOPROP ~ TRAT, data = datosT, contrasts = list(TRAT = mat))
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -0.4149 -0.1741 -0.0525  0.1776  0.5264 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.65469    0.02812   23.28  < 2e-16 ***
## TRATc1       1.92323    0.11932   16.12  < 2e-16 ***
## TRATc2       0.23213    0.06889    3.37  0.00124 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.2386 on 69 degrees of freedom
## Multiple R-squared:  0.7971, Adjusted R-squared:  0.7913 
## F-statistic: 135.6 on 2 and 69 DF,  p-value: < 2.2e-16

# cálculo de contrast (opción 2)
contrasts(TRAT) <- cbind(mat)
contraste <- aov(LOPROP ~ TRAT); summary.lm(contraste)

## Call:
## aov(formula = LOPROP ~ TRAT)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -0.4149 -0.1741 -0.0525  0.1776  0.5264 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.65469    0.02812   23.28  < 2e-16 ***
## TRATc1       1.92323    0.11932   16.12  < 2e-16 ***
## TRATc2       0.23213    0.06889    3.37  0.00124 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.2386 on 69 degrees of freedom
## Multiple R-squared:  0.7971, Adjusted R-squared:  0.7913 
## F-statistic: 135.6 on 2 and 69 DF,  p-value: < 2.2e-16

# medias de tratamientos solarizados
library(psych)

describeBy(PROP, TRAT, mat = TRUE, digits = 2)

##     item        group1 vars  n  mean    sd median trimmed   mad min  max
## X11    1 Sin solarizar    1 24 22.70 15.86  16.45   20.27 10.16 6.6 65.4
## X12    2  Solarizado 1    1 24  2.40  2.28   1.35    2.13  1.26 0.2  7.3
## X13    3  Solarizado 2    1 24  0.81  0.87   0.50    0.70  0.52 0.0  2.8
##     range skew kurtosis   se
## X11  58.8 1.32     0.88 3.24
## X12   7.1 1.02    -0.45 0.46
## X13   2.8 1.16     0.05 0.18

library(doBy)

library(pastecs)

summaryBy(PROP ~ TRAT, data = datosT, FUN = stat.desc)

##            TRAT PROP.nbr.val PROP.nbr.null PROP.nbr.na PROP.min PROP.max
## 1 Sin solarizar           24             0           0      6.6     65.4
## 2  Solarizado 1           24             0           0      0.2      7.3
## 3  Solarizado 2           24             4           0      0.0      2.8
##   PROP.range PROP.sum PROP.median PROP.mean PROP.SE.mean PROP.CI.mean.0.95
## 1       58.8    544.8       16.45   22.7000    3.2365161         6.6952436
## 2        7.1     57.6        1.35    2.4000    0.4648126         0.9615381
## 3        2.8     19.5        0.50    0.8125    0.1778813         0.3679755
##      PROP.var PROP.std.dev PROP.coef.var
## 1 251.4008696   15.8556258     0.6984857
## 2   5.1852174    2.2771072     0.9487947
## 3   0.7594022    0.8714368     1.0725377

Códigos en SAS

/***********************************************************

EXPERIMENTACIÓN EN AGRICULTURA

Fernández Escobar, R.; Trapero, A.; Domínguez, J. 2010

CAPÍTULO 13: ANÁLISIS DE LA VARIANZA COMBINADO

(páginas 167 - 172)

************************************************************/

DATA datos;

DO TRAT = 0 TO 2;

DO REP = 1 TO 4;

DO MUES = 1 TO 6;

INPUT PROP @@;

OUTPUT;

END;

LABEL TRAT = 'Tratamientos del suelo'

REP = 'Repeticiones'

MUES = 'Muestras de suelo'

PROP = 'Propágalos de V. dahliae (g/suelo)';

DATALINES;

18.4 19.8 23.6 60.2 34.5 15.7

28.3 65.4 23.1 34.5 9.6 16.4

13.4 12.0 7.1 15.0 9.6 45.3

16.5 8.1 12.7 15.8 6.6 33.2

0.6 1.5 1.1 6.2 0.5 0.2

0.7 2.7 1.2 4.4 7.3 0.5

7.0 3.6 0.8 0.5 1.2 0.9

2.3 0.8 3.7 1.9 6.5 1.5

2.8 1.2 0.6 0.9 0.0 0.3

0.0 0.2 0.4 2.6 0.3 0.5

1.0 2.7 1.8 0.5 0.0 0.8

0.5 1.6 0.4 0.2 0.2 0.0

;

ODS HTML;

* Mostrar datos;

PROC PRINT DATA = datos;

RUN;

* Etiquetar TRATAMIENTOS;

PROC FORMAT;

VALUE TRATCODIGO

0 = 'Sin solarizar'

1 = 'Solarizado 1'

2 = 'Solarizado 2';

RUN;

DATA datosID;

SET datos;

FORMAT TRAT TRATCODIGO. REP MUES PROP;

RUN;

* Datos con ID ;

PROC PRINT DATA = datosID;

RUN;

* Transformación logarítmica (LOPROP);

DATA datosT;

SET datosID;

LOPROP = log10(PROP+1);

LABEL = 'log(# propagalos)';

RUN;

* Datos + variable transformada;

PROC PRINT DATA = datosT;

RUN;

* Estadísticas descriptivas;

PROC MEANS MEAN STD STDERR;

VAR PROP LOPROP;

CLASS TRAT REP;

RUN;

* Opción 1: ANOVA bloques divididos;

PROC GLM DATA = datosT;

CLASS TRAT REP MUES;

MODEL LOPROP = REP TRAT TRAT*REP / SS3;

TEST H =TRAT REP E = TRAT*REP;

RUN;

* Opción 2: ANOVA bloques divididos;

PROC MIXED DATA = datosT METHOD = TYPE3;

CLASS TRAT REP MUES;

MODEL LOPROP = TRAT REP TRAT*REP*MUES/DDFM=SATTERTH;

RANDOM REP*TRAT;

RUN;

PROC GLM;

CLASS TRAT REP;

MODEL LOPROP = TRAT REP;

MEANS TRAT;

CONTRAST 'No solarizado vs. (Solarizado 1 + Solarizado 2)' TRAT 2 -1 -1;

CONTRAST 'Solarizado 1 vs. Solarizado 2' TRAT 0 1 -1;

RUN;

PROC MEANS MEAN STD;

VAR PROP;

CLASS TRAT;

RUN;

ODS HTML CLOSE;

------------------------------------------------------------

Archivos: tabla 13.1.csv, capítulo 13a.R, summarySE.R, capítulo 13a.sas

Estudiando Agricultura en Taiwán

Páginas

marzo 14, 2017

ANOVA combinado (1) — un muestreo

No hay comentarios:

Publicar un comentario